きのこはどうやって胞子を遠くに飛ばすのか?(2)

Twitterにて役に立たないきのこ氏が「(流体力学的)きのこの仮説」というコラムを書いた、というTweetが流れてきた。
実はこれ、以前から気になっていたのですが、まったく手を付けられずにいました。そんな僕にとって「我が意を得たり」と思い読み進めて行った記事は、僕の想像の遥か3000m以上上空を飛んでおりました (@_@;)
この記事は役に立たないきのこ氏から許可を得て、画像、文章を転載させていただくことになったものです。また転載の際には僕なりの批評も付けてね、と言われちゃいましたので最後にちょこっと感想も付け加えておりますので、最後までお読みください。
(流体力学的)きのこの第1仮説
【注意】
この話は科学に無知な筆者が付け焼き刃の知識を基に書いた、いわゆるエセ科学と同等の記事で、内容的な正確性は未検証です。

きのこには様々な形のものがありますが、中でも目立つのはドーム状の傘を持ったものでしょう。[Fig.1-1] これには胞子を雨の直撃から守るとともに、胞子(担子器)を広い面積に配置できる長所があると思われますが、胞子を風で拡散させるという目的に対してはどんな効果があるでしょうか。
序章(第0仮説)ではしばしば見受けられる揚力説に疑問を投げかけましたが、まず揚力の話は一旦忘れて、ドーム状の物体に風が当たった時に空気の流れがどうなるのかを一から考えてみましょう。

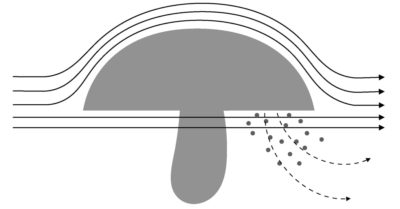
話を単純化するために、きのこの周囲の空気の流れが周囲の草などによってかき乱されていない、整った気流(層流)であると仮定します。この時流体の粘度が極めて低ければ(レイノルズ数が小さい)、気流は層流のまま曲面に沿って流れて行きます。[Fig.1-2]

しかし実際には空気には粘性があるため、表面付近では流れの遅い層(境界層)ができます。境界層は表面に近いほど速度が遅いために速度勾配により摩擦抵抗が生じますが、流れは摩擦抵抗により次第に速度が落ち、ある点に達すると流れが抵抗に負けて速度が0になり、さらに先では逆転してしまうのです。[Fig.1-3]
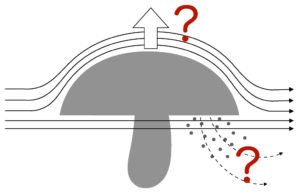
この時、流れが逆転した部分では層流とは逆方向の流れが発生し、層流は表面から引き剥がされてしまいます(はく離)。はく離が起きるとその後方では不規則な渦が発生(乱流)が発生します。[Fig.1-4]

そしてこれからが本題です。傘の下側から放出された胞子は、Fig.1-2のようにもし乱流が発生しなかった場合、真横に流されると予想されます。これでも無風状態よりは遠くに胞子を飛ばすことが可能ですが、全く乱れのない層流では上に舞い上がることはなく、緩やかに放物線を描きながら下に落ちて終わるのではないでしょうか。
しかし、風下側に大きな乱流が発生している場合、層流との境界でも流れが不規則に混じり合い、横に流された胞子が巻き上げられて、より遠くに飛ばされる可能性が出てくるのではないでしょうか。
これが流体力学的きのこの第1仮説、きのこの傘の風下側に発生した乱流により、傘裏から放出された胞子が巻き上げられるというものです。いかがでしょうか。
【この仮説における問題点】
- 森や草むらに生えているきのこに対して、層流をモデルとして説明することが適切なのか
- 層流、乱流、はく離は航空機など高速移動する物体を説明するものであるが、これを微風下で静止したきのこに適用するのが正しいのか
編集後記
さて、今回のコラムは良く読まないとかなり理解することが難しいのではないでしょうか?しかし今回のコラムが後のコラムの下敷きとなりますので、できればちゃんと理解できるまで読んでもらった方がいいかもしれません。まずは「層流」という空気の流れがある、ということ。空気はキノコの傘に沿って流れようとします。もしキノコの傘が綺麗な流線形であり、空気に粘性がなければ空気はそのまま後ろに流されていくことでしょう。
しかし、空気に粘性があること、そして傘表面との摩擦があること、これにより空気の流れに速い部分と遅い部分が生じますね。これは川の流れと同じで、川岸に近い水の流れと、川の中央の流れの速さでは中央の方が圧倒的に速くなります。それと同じで傘の近くになればなるほど空気の流は遅くなります。
それにより空気の流れの中に渦が発生します。
頭の中に鳴門の渦潮を頭の中に想像してください(笑)。
この渦というものは2つの流れを生みます。1つめは渦の中に巻き込まれ、渦自身になってしまう流れ、もう一つは渦から離れていく流れです。この2つの流れが生まれることを「はく離」と言います。
そして渦によって作られた乱れた流れ(これを乱流と言います)は傘の下を通ってきた流れと合流し、下を通ってやってきた胞子を乱流によって巻き上げられ遠くに飛ばされる、、、という推測ですね、とっても素晴らしい仮説だと思います。
また一つ付け加えるなら、傘の形がまんじゅう型であればあるほどこの渦は起きやすく(すなわちはく離が起きやすい)、より遠くへ飛んでいくのではないかと思われますので、大きな胞子のものはより傘をまんじゅう型にする必要があるかもしません。
おっと、これ以上言うと、役に立たないきのこさんにツッコまれそうなので、この辺で(笑)
いりさじょうじ
【参考文献】(敬称略)
『流れのふしぎ』遊んでわかる流体力学のABC
日本機械学会編 石綿良三・根本光正著(講談社ブルーバックス)
『鳩ぽっぽ』初心者のための航空力学講座
Oki (https://pigeon-poppo.com)
『機械設計エンジニアの基礎知識』流体力学の基礎を学ぶ
MONOWEB (https://d-engineer.com/monoweb.html)
『楽しい流れの実験教室』
日本機械学会 流体工学部門 (https://www.jsme-fed.org/experiment/index.html)